برای محاسبه ی ریشه ی سوم باید توان 3 این اعداد را بدانید :
=1
= 8
= 27
= 64
= 125
= 216
= 343
= 512
= 729
= 1000
با دانستن مکعب این اعداد محاسبه ی ریشه ی سوم این اعداد مثل آب خوردن می شود .
با یک مثال شروع می کنیم :
ریشه ی سوم 314432 چند است ؟
مرحله به مرحله جلو می رویم :
1- رقم هزارگان عدد را در نظر بگیرید . در این مثال 314 .
2- چون 314 بین =216 و = 343 است پس طبق جدول توان 3 ریشه ی سوم
باید شصت و ... باشد . اولین رقم ریشه ی سوم 6 است .
3- برای تعیین رقم آخر ریشه ی سوم ، توجه کنید که تنها مکعب عدد 8 است که به 2 ختم می شود =512 پس ریشه ی سوم عدد 314432 عدد 68 است . به همین راحتی !
توجه کنید که ارقام صفر تا 9 رقم آخر مکعب اعداد 0 تا 10 را تشکیل می دهند .
حالا این یکی را امتحان کنید :
ریشه ی سوم 19683 چند است ؟
1- 19 بین 8 و 27 است .
2- از این رو ریشه ی سوم بیست و ... است .
3- رقم آخر عدد 3 است ، مثل رقم آخر =343 ، پس 7 رقم آخر است ، یعنی 27 ریشه ی سوم این عدد است .
یادتان باشد که در اینجا روش ما برای به دست آوردن رقم آخر تنهادر صورتی جواب می دهد که عدد اصلی مکعب کامل باشد .
وزن فیل = وزن پشه

ادعا:
وزن فیل = وزن پشه
اما چه طور این ادعا را ثابت کنیم :
اگر x وزن فیل و y وزن پشه باشدو قرار دهیم



از ضرب این رابطه ها خواهیم داشت:

در نتیجه :

با اضافه کردن  به دو طرف داریم :
به دو طرف داریم :

و لذا

بنابراین

پس

و این یعنی

وقتی من به دنیا اومدم پدرم 30 سالش بود یعنی سنش 30 برابر من بود وقتی من 2 ساله شدم پدرم 32 ساله شد یعنی 16 برابر من وقتی من 3 ساله شدم پدرم 33 ساله شد یعنی 11 برابر من وقتی من 5 ساله شدم پدرم 35 ساله شد یعنی 7 برابر من وقتی من 10 ساله شدم پدرم 40 ساله شد یعنی 4 برابر من وقتی من 15 ساله شدم پدرم 45 ساله شد یعنی 3 برابر من وقتی من 30 ساله شدم پدرم 60 ساله شد یعنی 2 برابر من می ترسم اگه ادامه بدم از پدرم بزرگتر بشم . از دکتر علی شریعتی
مسلما 1 مساوی با 1 است اما عکس زیر کاملا منطقی نشان دهنده آن است که یک مساوی با 2 است. آیا کسی میتواند بگوید که چه ترفندی در اینجا به کار رفته و یا شاید هم ترفندی در کار نبوده و 1 مساوی با 2 است!!!

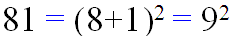
بله 81 برابر است با توان دوم ِ مجموع ارقامش.
آیا اعداد دیگری با این ویژگی وجود دارند؟
به عدد زیر نیز توجه کنید :

حتما ً شگفت زده شده اید !
در این قسمت می خواهیم اعدادی را معرفی کنیم که این اعداد با توانی از مجموع ِ ارقامشان برابرند. البته در این میان، اعداد یک رقمی با مجموع ارقامشان به توان 1 برابند و از آن ها چشم پوشی می کنیم. یافتن اعداد کوچک با این ویژگی کار ساده ای است اما یافتن اعداد بزرگتر بسیار مشکل و زمان بر خواهد بود. در جدول زیر تعدادی از این اعداد را به نمایش در آورده ایم . ببینید و لذت ببرید :
|
|
= |
عدد |
|
92 |
= |
81 |
|
83 |
= |
512 |
|
173 |
= |
4913 |
|
183 |
= |
5832 |
|
263 |
= |
17576 |
|
273 |
= |
19683 |
|
74 |
= |
2401 |
|
224 |
= |
234256 |
|
254 |
= |
390625 |
|
284 |
= |
614656 |
|
364 |
= |
1679616 |
|
285 |
= |
17210368 |
|
355 |
= |
52521875 |
|
365 |
= |
60466176 |
|
465 |
= |
205962976 |
|
186 |
= |
34012224 |
|
456 |
= |
8303765625 |
|
546 |
= |
24794911296 |
|
646 |
= |
68719476736 |
|
187 |
= |
612220032 |
|
277 |
= |
10460353203 |
|
317 |
= |
27512614111 |
|
347 |
= |
52523350144 |
|
437 |
= |
271818611107 |
|
537 |
= |
1174711139837 |
|
587 |
= |
2207984167552 |
|
687 |
= |
6722988818432 |
|
468 |
= |
20047612231936 |
|
548 |
= |
72301961339136 |
|
638 |
= |
248155780267521 |
سال ها پیش در یکی از کلاس های ریاضیات مدارس آلمان، آموزگار برای اینکه مدتی بچه ها را سرگرم کند و به کارش برسد؛ از آنها خواست تا مجموع اعداد از یک تا صد را حساب کنند. پس از چند دقیقه یکی از شاگردان کلاس گفت: مجموع این اعداد را پیدا کرده و حاصل عدد 5050 می شود. با شنیدن این عدد معلم با حیرت فراوان او را به پای تخته برد تا روش محاسبه خود را توضیح دهد. به نظر شما این شاگرد باهوش که بعدها یکی از بزرگ ترین و معروف ترین ریاضیدانان دنیا شد.
چه روشی را به کار بست؟ او اعداد یک تا صد را به ردیف پشت سرهم نوشت، سپس بار دیگر همین اعداد را بالعکس، این بار از صدتا یک، درست در ردیف زیرین اعداد قبلی نوشت. طوری که هر عدد زیر عدد ردیف بالاتر قرار گرفت.وی مشاهده کرد که مجموع هر کدام از ستون های به وجود آمده 101 است. سپس نتیجه گرفت که صد تا عدد 101 داریم که حاصل مجموع آنها می شود 10100=101*100. پس از آن تنها کافی بود که این مجموع به دست آمده نصف شود یعنی:
5050 = 2 / 10100
شاید «شارل فردریک گاوس» شاگرد با ذکاوت کلاس که این روش جالب را به کاربرد، آن هنگام نمی دانست، روش بسیار کارا و مفیدی را برای جمع بستن رشته ای از اعداد ارائه داده است که تا سالیان سال مورد استفاده ریاضیدانان خواهد بود.اکثر مفاهیم ریاضی به قدری با زندگی روزمره ما گره خورده است که تمام مردم بدون آگاهی داشتن و واقف بودن به آن، از کنارش می گذرند و تنها کاربر خوبی هستند و بس!
1) هر یک از عبارت های زیر را طوری پرانتز گذاری کنید تا تساوی برقرار شود.
مثال: 8 = ( 1 + 3 ) × 2 8 = 1 + 3 × 2
6 = 2 + 3 ÷ 6 + 24 (ب 4= 1 + 3 × 2 ÷ 28 ( الف
1 = 6 ÷ 12 + 8 ÷ 40 × 3 ( د 20 = 3 - 15 ÷ 25 × 3 + 18 ( ج
2)در بین اعداد، عمل ها را طوری قرار دهید تا یک رابطه تساوی به دست آید.
مثال: 7 = 1 + 3 × 2 ( = + × ) 2 ، 7 ، 1 ، 3
( = + ÷ ) 2 ، 5 ، 10 ، 4 (الف
( = + × ) 7 ، 5 ، 3 ، 2 (ب
( = × - ÷ ) 6 ، 3 ، 24 ، 8 ، 4 (ج
محاسبه عجیب:
از پدری پرسیدند: آیا درست است که می گویند:(زمانی فرا خواهد رسید که پسرها بزرگتر ازپدرشان خواهند شد؟)گفت:اتفاقا این موضوع سخت ذهن مرا به خود مشغول کرده است.
البته کاری به استعداد ونبوغ شان ندارم.منظور من سن وسال آنهاست.....
پرسیدند:به چه دلیل؟
گفت:به این دلیل که برایتان شرح خواهم داد.
وقتی پسرم متولدشد من30 سال داشتم.یعنی 30 برابر او سن داشتم.
وقتی 2 ساله شدمن32 سال داشتم.یعنی16 برابراوسن داشتم.
وقتی3 ساله شدمن33 سال داشتم.یعنی11 برابر او سن داشتم.
وقتی5 ساله شدمن35 سال داشتم.یعنی7 برابر او سن داشتم.
وقتی6 ساله شدمن36 سال داشتم.یعنی6 برابر او سن داشتم.
وقتی10 ساله شدمن40 سال داشتم.یعنی4 برابر او سن داشتم.
وقتی15 ساله شدمن45 سال داشتم.یعنی3 برابراو سن داشتم.
حالا او30 ساله شده است ومن60 سال دارم یعنی 2 برابر اوسن دارم.
می ترسم اگر اوضاع به همین منوال پیش رود او به زودی ازمن جلو بزند و اوپدر من یشود و من پسر اوبشوم.
.: Weblog Themes By Pichak :.

